O que é um coeficiente de variação?
Antes de você iniciar a leitura, eu preciso te dar um spoiler: o coeficiente de variação, tema deste post, é calculado a partir da média e do desvio-padrão. O texto vai assumir que você tem familiaridade com o conceito de desvio-padrão. Se não for o seu caso, recomendo que você leia antes o post que explica o que é e como interpretar o desvio-padrão, combinado?
Um breve resumo sobre variância e desvio-padrão
No post anterior, sobre variância e desvio-padrão, nós discutimos que:
- Variância e desvio-padrão são medidas de dispersão que quantificam o quão dispersos os dados estão em relação à média
- Quanto maior a variância ou o desvio-padrão, mais dispersos estão os dados – ou seja, mais eles variam
- A unidade de medida da variância é a unidade original elevada ao quadrado, o que a torna uma medida muito mais difícil de interpretar que o desvio-padrão, que está na unidade de medida original
Hoje vamos conversar sobre uma outra medida de dispersão, o coeficiente de variação. Mas, para esse coeficiente fazer sentido, vou partir de um exemplo – um exemplo um pouco estranho, mas vou te pedir para confiar na minha construção de raciocínio, ok?
O que varia mais? A altura de mulheres ou de gatos domésticos?
Vamos imaginar que estamos interessados em comparar as variações nas alturas de mulheres e de gatos. Para isso, aferimos as alturas de duas amostras: uma composta por 10 mulheres e outra composta por 10 gatos. As alturas que encontramos estão detalhadas a seguir:
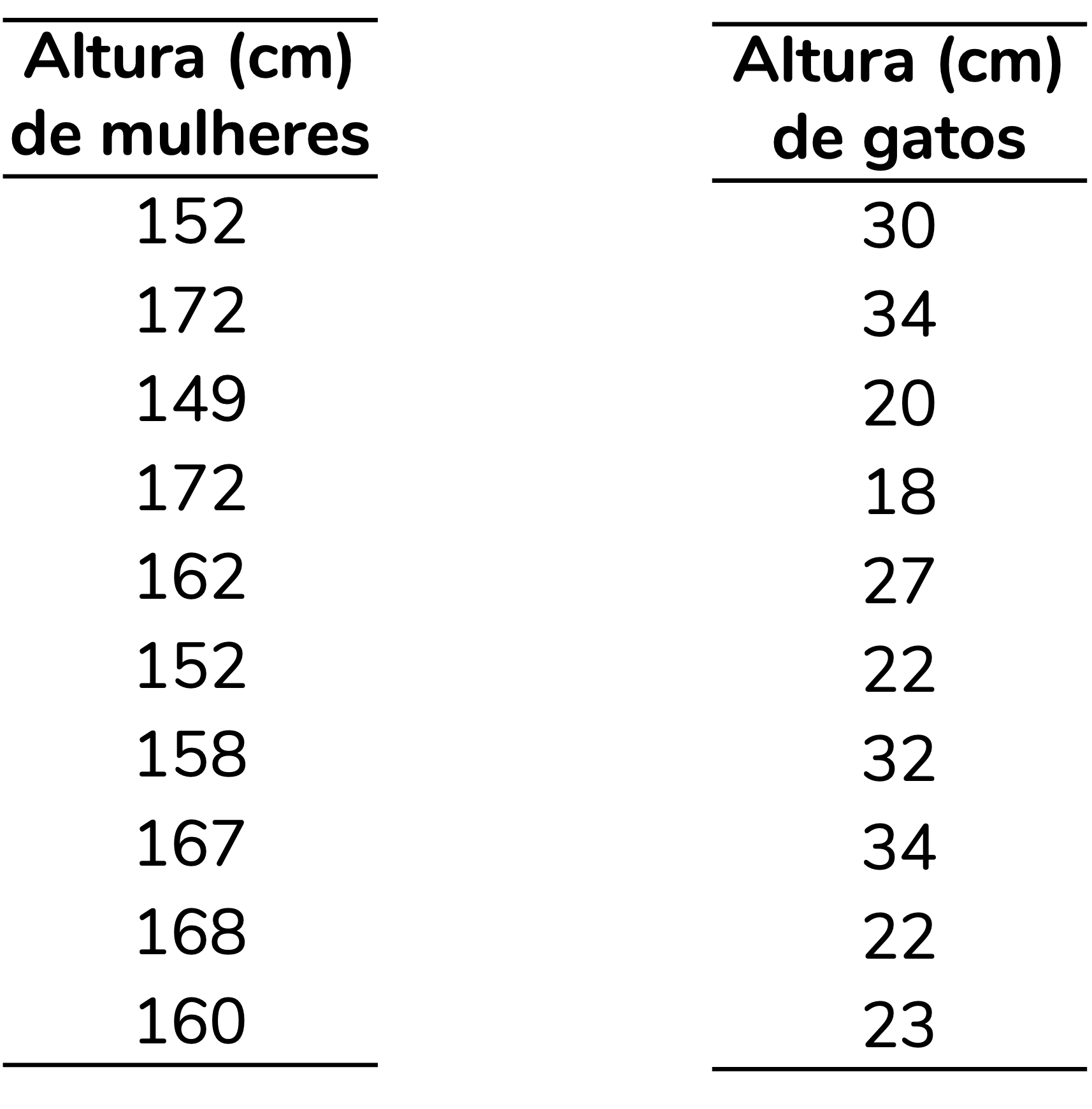
Se estamos interessados na variação dos dados, podemos calcular o desvio-padrão para cada uma dessas amostras, seguindo exatamente os passos que discutimos no post anterior. Claro, poderíamos também calcular a variância, mas aqui vou focar no desvio-padrão por ser uma medida mais interpretável. As médias e desvios-padrão para cada uma dessas amostras estão representados abaixo:
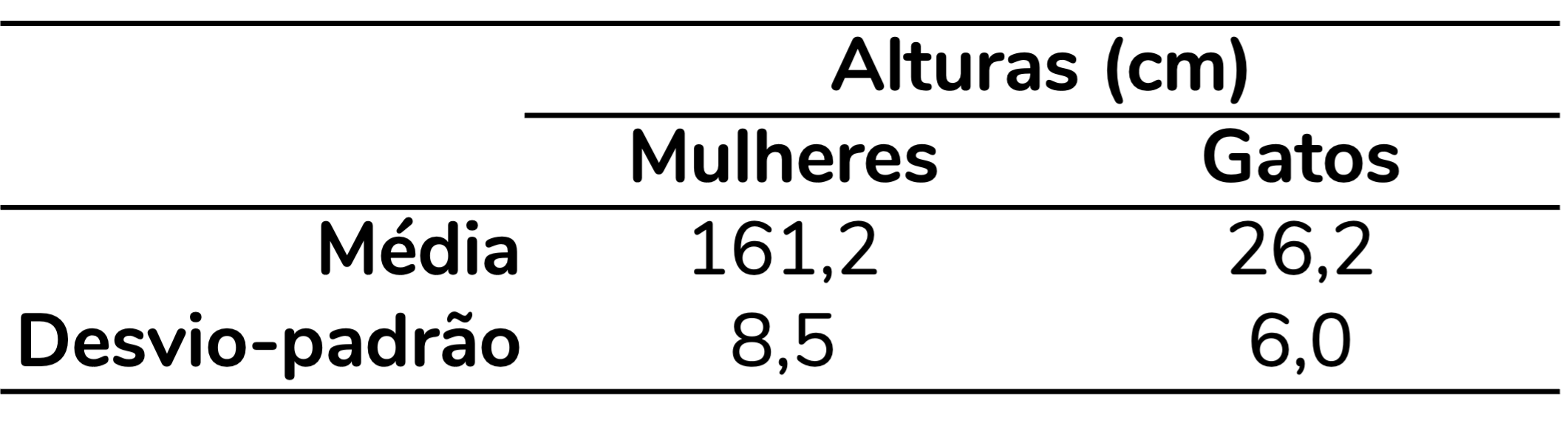
O desvio-padrão calculado nos indica que as alturas das mulheres estão variando, em média, 8,5 cm para mais ou para menos, em relação à média da amostra, que é 161,2 cm. Já as alturas dos gatos estão variando 6,0 cm, para mais ou para menos, em relação à sua média de 26,2 cm.
Podemos, agora, voltar à pergunta que abriu esse tópico: quais alturas variam mais em relação à média? As de mulheres ou as de gatos?
Perceba que os desvios-padrão estão na mesma unidade de medida (cm). Portanto, uma possibilidade seria compará-los. Como o desvio-padrão para mulheres é maior, podemos dizer que as alturas das mulheres variam mais em relação à média do que as alturas dos gatos.
Mas você pode estar pensando: poxa, mas variar 6 cm em relação a 26,2 cm parece uma variação muito maior do que variar 8,5 cm em relação a 161,2 cm! E você tem razão nesse raciocínio.
Visualizando a variação nas duas amostras
Para entender isso melhor, vamos visualizar essa variação. Nos dois gráficos abaixo, a barra central se refere à média de altura daquela amostra (mulheres no gráfico à esquerda e gatos à direita), a barra à esquerda corresponde à média menos um desvio-padrão (DP) e a barra à direita corresponde à média mais um DP.
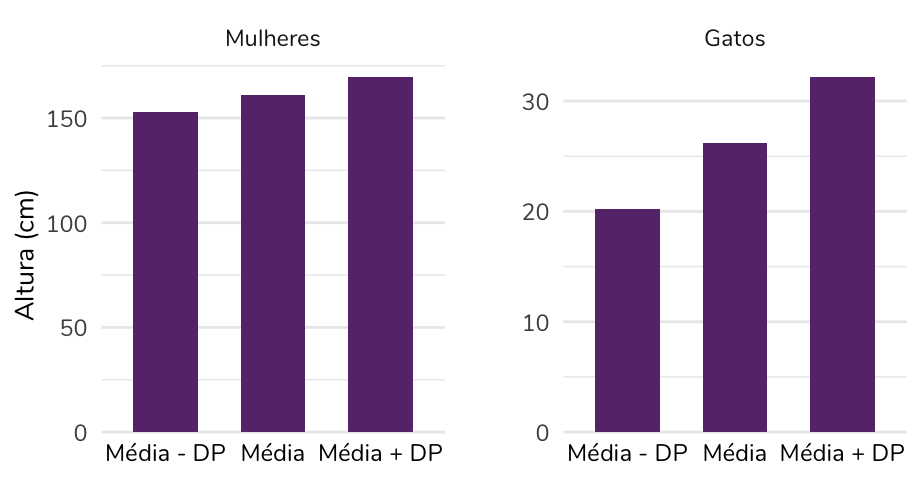
Perceba como o desvio-padrão das alturas das mulheres corresponde a uma variação muito menor – em termos relativos – que o desvio-padrão das alturas dos gatos. Tá, mas como avaliar essa variação em termos relativos? Uma das formas é pensarmos percentualmente.
Calculando e interpretando o coeficiente de variação
A lógica aqui é pensar: o desvio-padrão calculado corresponde a quantos porcento da média? Por exemplo, se a média for 20 cm e o desvio-padrão for 10 cm, então o desvio-padrão é metade da média. O que significa dizer que o desvio-padrão é 50% da média (1/2 = 0,5 = 50%).
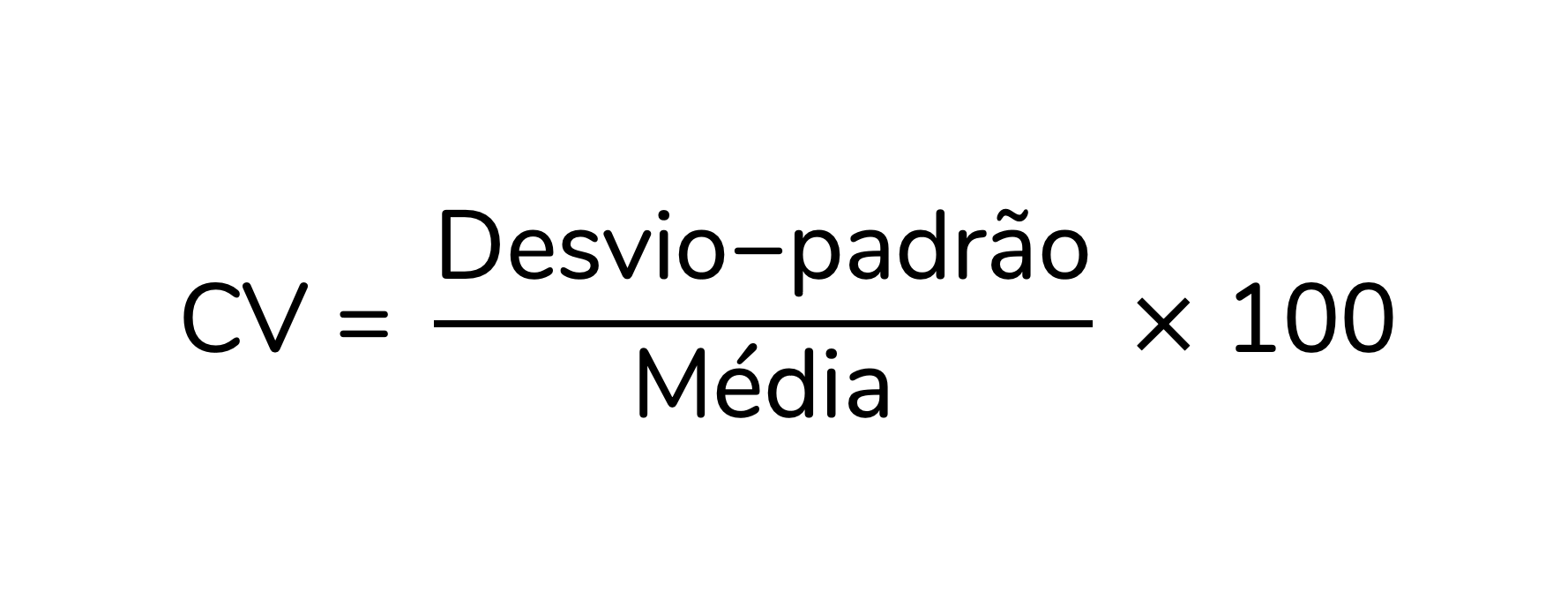
O coeficiente de variação (CV) faz exatamente esse cálculo. Para calcularmos o CV, devemos dividir o desvio-padrão pela média. Além disso, geralmente multiplicamos esse resultado por 100, para facilitar a sua interpretação como porcentagem.
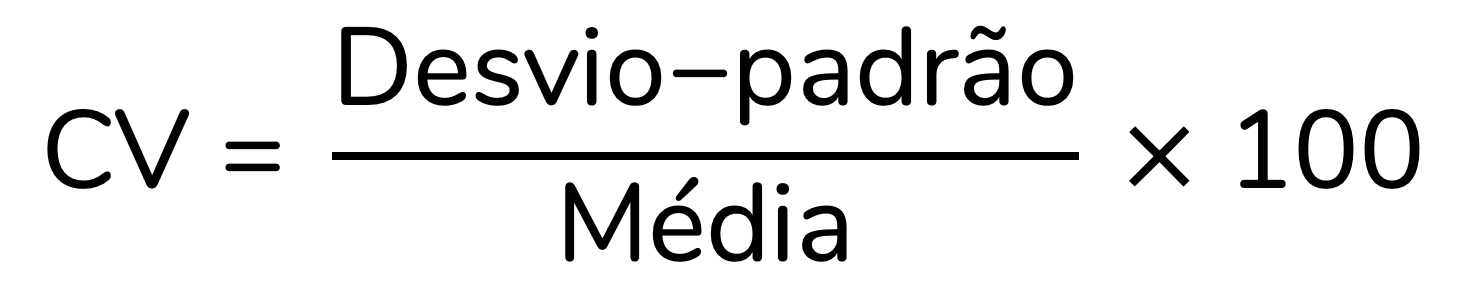
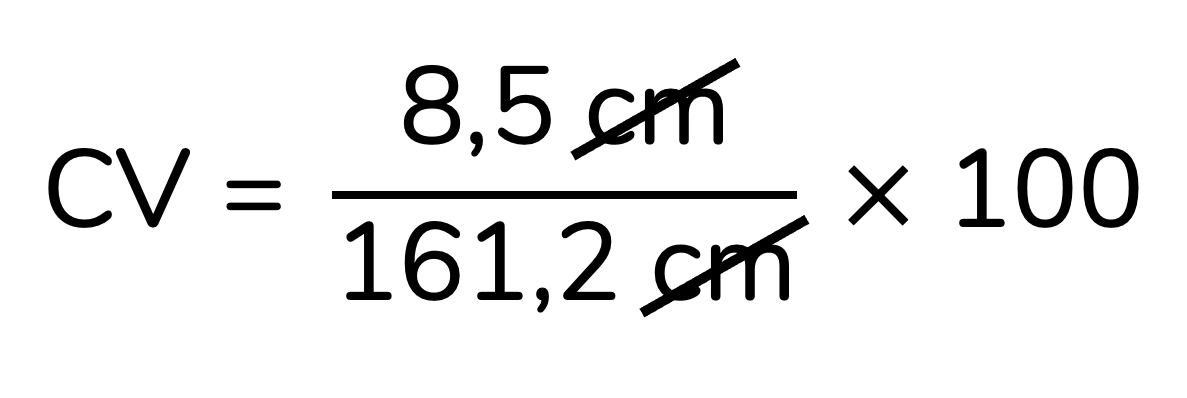
Vamos aplicar esse cálculo às nossas amostras, e interpretar o coeficiente de variação (CV) obtido. Para mulheres, o cálculo será:

Já para gatos, o cálculo do coeficiente de variação (CV) resultará em…

Ok, vamos agora interpretar esse resultados:
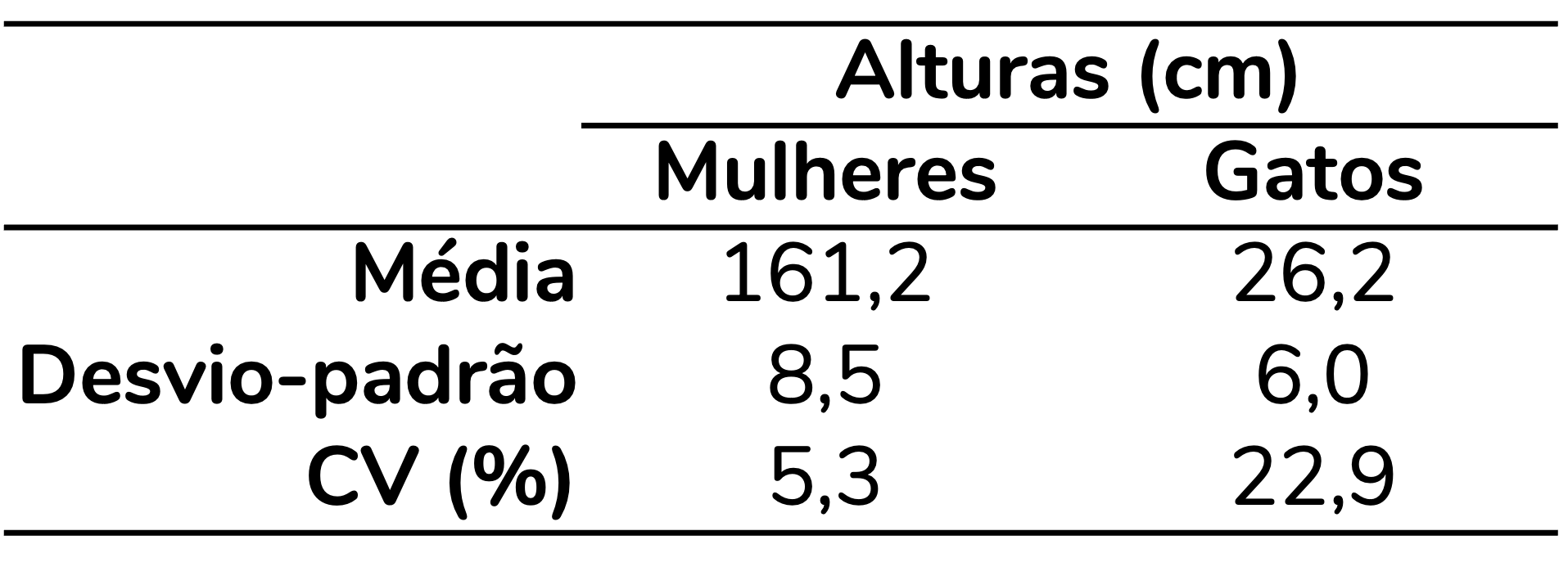
O coeficiente de variação nos indica que as alturas das mulheres estão variando, em média, 5,3% em relação à média. Já as alturas dos gatos variam 22,9% em relação à sua média. Portanto, se pensarmos em termos relativos – isso é, percentualmente – as alturas dos gatos variam mais.
Quando faz sentido usar o coeficiente de variação?
Como conversamos, o coeficiente de variação fornece uma informação sobre a variação dos dados em termos relativos, percentuais. Um coeficiente de variação de 10%, por exemplo, indica que o desvio-padrão corresponde a 10% da média. Mas, você pode estar se perguntando: em quais situações faz sentido calcular o coeficiente de variação? Bom, a resposta óbvia é: quando o seu interesse é avaliar essa variação em termos relativos. Mas vou detalhar duas situações nas quais esse tende a ser o nosso interesse.
Quando os grupos apresentam médias muito diferentes
O exemplo de comparar as alturas de mulheres e gatos não está aqui por acaso. Perceba que são grupos com médias de altura muito diferentes. A média de altura das mulheres é mais de seis vezes a média de altura dos gatos. Por isso, soa estranho, até “injusto”, comparar os desvios-padrão – ou seja, comparar uma medida absoluta de variação. O coeficiente de variação resolve esse problema ao permitir que a gente compare o quanto cada grupo está variando usando a média desse grupo como “escala”.
Então, um dos principais uso do coeficiente de variação é na comparação de grupos com médias muito diferentes.
Quando queremos comparar desvios-padrão que estão em unidades de medida diferentes
Perceba que o coeficiente de variação (CV) é uma medida de dispersão adimensional, isso é, sem unidade de medida. Isso porque, ao calcularmos o CV, dividimos o desvio-padrão pela média. E, lembre-se, o desvio-padrão e a média estão na mesma unidade de medida. Ao dividirmos um pelo outro, essas unidades “se cancelam”.
Já discutimos como o coeficiente de variação é uma medida útil para compararmos a dispersão de grupos com médias muito diferentes, ainda que na mesma unidade de medida (como as alturas de mulheres em gatos, ambas em cm). Mas, por ser adimensional, o coeficiente de variação é também uma excelente forma de compararmos dispersões quando temos dados em unidades de medida diferentes.
Alguns cuidados!
O coeficiente de variação não é adequado para algumas variáveis
Muiros autores dirão que o coeficiente de variação só pode ser calculado para variáveis de razão, que apresentam um zero absoluto (Abdi, 2010; Fávero; Belfiore, 2017; Santos; Dias, 2021). Ok, mas o que isso significa?
Podemos dividir as variáveis numéricas em variáveis de intervalo e variáveis de razão (Fávero; Belfiore, 2017). A diferença entre elas é que apenas as variáveis de razão apresentam um zero absoluto. Para isso fazer sentido, vamos pensar em temperaturas. Se aferimos uma temperatura em graus Celsius (°C), o zero (0°C) não indica ausência de temperatura. A escolha do zero é arbitrária. Por isso, a temperatura em Celsius está em uma escala intervalar. O mesmo vale para a temperatura em Fahrenheit (°F): há um zero arbitrário, que não indica ausência de temperatura. Portanto, Fahrenheit também é uma escala intervalar. Por outro lado, a temperatura em Kelvin (K) apresenta um zero absoluto: 0K corresponde a ausência de temperatura. Logo, a temperatura em Kelvin está em uma escala de razão.
A forma como interpretamos dados em escalas intervalares e de razão também é ligeiramente diferente. Se estamos trabalhando com uma escala de razão, como Kelvin, em que há um zero absoluto, podemos dizer que:
- A diferença de temperatura entre 10K e 20K é a mesma que entre 35K e 45K, por exemplo
- A temperatura 20K é o dobro da temperatura 10K
Se estamos falando de um dado medido em uma escala intervalar, a primeira frase se mantém, mas a segunda não. Por exemplo, para graus Celsius podemos dizer que:
- A diferença de temperatura entre 10°C e 20°C é a mesma que entre 35°C e 45°C
Mas, não podemos dizer que 20°C é o dobro da temperatura 10°C. Isso porque como não há um zero absoluto, não podemos dizer que um intervalo específico é multiplo de outro (Fávero; Belfiore, 2017).
Em geral, as análises e estatísticas descritivas que usamos para variáveis intervalares e de razão são as mesmas. Mas, o coeficiente de variação é uma exceção. Esse coeficiente deveria ser calculado apenas para dados em escala de razão.
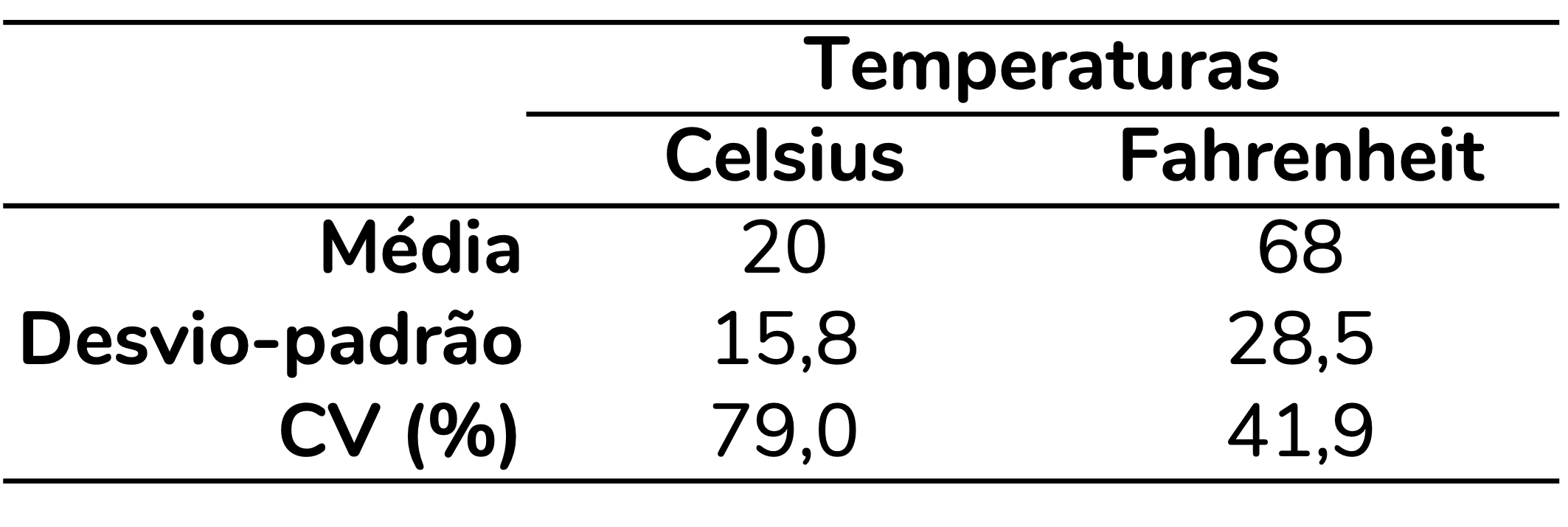
Aqui preciso compartilhar que um exemplo que me fez enxergar o problema de usarmos dados intervalares para calcular o coeficiente de variação é o que consta na página sobre coefiente de variação da Wikipedia. Vou discutir uma versão simplificada aqui. Imagine que temos uma base de dados com cinco temperaturas em °C: 0, 10, 20, 30 e 40. Para representar essas mesmas temperaturas em Fahrenheit, devemos multiplicar cada valor em Celsius por 9/5 e então somar 32 ao resultado. Isso resulta nos valores representados na tabela abaixo:

Se os dados são exatamente os mesmos, apenas em escalas diferentes, esperaríamos um mesmo coeficiente de variação, certo? Mas… Isso não acontece:
Além disso, alguns autores dirão que o coeficiente de variação pode ser utilizado apenas quando todos os valores do conjunto são positivos (Abdi, 2010). Outros dirão que o coeficiente de variação pode ser calculado quando há valores negativos, mas apenas quando todos os valores do conjunto de dados são negativos (Santos; Dias, 2021). E, nesses casos, para calcular o coeficiente de variação devemos dividir o desvio-padrão pelo módulo – isso é, pelo valor absoluto – da média.
Mas, há aqui um consenso: não podemos usar o coeficiente de variação quando o conjunto de dados inclui valores positivos e negativos. Isso porque, nessas situações, o cálculo do coeficiente de variação resulta em uma valor que não segue interpretação que discutimos aqui.
A média não é tudo nessa vida
Já disse isso no post de desvio-padrão, e repito: nem sempre a média é a medida-resumo mais adequada a um conjunto de dados. A média é uma medida bem sensível a valores discrepantes (que chamamos em inglês de outliers). Lembre-se que o coeficiente de variação, assim como o desvio-padrão, é uma medida de dispersão baseada na média. Portanto, se a média não for uma representação adequada daquele conjunto de dados, o coeficiente de variação também não o será. Uma possibilidade nesses casos é calcular a amplitude interquartil, que eu discuto em detalhes aqui.
Como citar esse post, nas normas da ABNT
PERES, Fernanda F. O que é um coeficiente de variação?. Blog Fernanda Peres, São Paulo, 10 fev. 2025. Disponível em: https://fernandafperes.com.br/blog/coeficiente-de-variacao/.